Lecture 4 : Bayesian Classifiers (3)

Bayes Classifier의 단점(한계점)

베이즈 분류기를 사용할 때에는 주로 Poseterior Probability를 최대화 시켜주는 decision을 내리는데, posterior

 

probability를 직접적으로 구할 수 없기에 Bayes 정리를 이용하여 Likelihood function으로 대신 decision을 내린다. 

하지만 크게 두가지 문제가 존재하는데,

 

첫번째 문제는 Gaussian 분포를 따른다고 가정했던 likelihood들이 사실상 가우시안분포가 아닐 수도 있다는 것이다.

 

multivariate likelihood이지만 가우시안 분포를 따르지 않는 경우에는 거의 실현 불가능하다.

 

두번재 문제는 high dimension을 갖는 가우시안 분포의 경우 계산이 굉장히 복잡해진다는 것이다.

 

 

손으로 필기한 숫자를 분류기를 사용하여 구분해내는 경우를 예시로 생각해보자.

30 by 30의 픽셀들은 모두 0 또는 1의 값을 갖는 랜덤 변수이며 이러한 pixel이 900개의 차원을 갖는 input이 될것이다. 

 

단순하게 이 입력값이 5인지 6인지 두가지 class를 구분하는 문제라고 생각을 해보면, 일단 입력이 들어왔을 때, 이 값이

 

5가될지 6이될지를 나타내주는 posterior probability를 먼저 구해줘야한다.

 

일단 Prior probability를 특정해주기 위해서는 c개의 클래스가 존재하는 경우에는 c-1개의 파라미터가 필요하다.

 

(ex. 5가 나올 확률을 p라고하면, 6이 나올 확률을 자연히 1-p이다. 따라서 a,b,c,....로 prior probability를 정해주면 나머지

 

한 클래스의 prior probability는 1-(a+b+c....)로 표현 가능하다. )

 

그렇다면 Likelihood를 특정해주기 위해서는 c개의 클래스가 존재하는 경우에는 c *(2^n -1)개의 parameter가 필요하다.

 

이러한 문제를 해결하기 위해서 등장한 것이 바로 Naive Bayes이다.

 

Naive Bayes는 모든 input feature들이 class conditionally independent하다는 것을 가정한다.

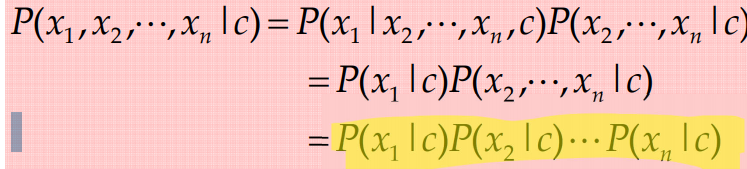
이렇게 independent assumption을 해주게 된다면, 필요한 파라미터의 수가 c * n개로 줄어들게 된다.