Lecture 5 : Logistic Regression & Maximum Likelihood Estimation (2)
Maximum Likelihood Estimation
likelihood(가능도)가 뭔지 알기 위해서는 probability(확률)와 likelihood(가능도)의 차이점에 대하여 구분해야한다.
probability는 고정된 분포, pdf에서의 면적을 의미한다. 이미 고정된, 구해진 분포에서 특정 데이터 값이 나올
확률, 즉 주어진 pdf의 면적을 의미한다.

하지만, likelihood는 특정 data point가 이 분포로부터 나왔을 가능도를 의미한다.
즉, 특정 data(고정된 값)에서의 추정 pdf의 높이(y값)을 의미한다.

L(theta; D) => 특정 data가 변할 수 있는 분포에서 나올 확률
이러한 likelihood를 수치적으로 구하는 방법?? 각 데이터 샘플들에서 후보로 사용되는 분포에 대한 높이(likelihood 기여
도)를 계산해서 모두 곱하는것

1, 4, 5, 6, 9라는 데이터가 주어져있을 때, 이러한 데이터들이 주황색의 가우시안 분포로 부터 나왔을 가능도를 구해보면,
주황색 분포의 pdf에 1, 4, 5, 6, 9라는 데이터 값을 넣었을 때의 y값(likelihood 기여도)를 모두 곱한 것이 likelihood.

theta는 주황색 분포의 parameter들 (Ex. 평균, 분산..)을 나타낸다. 즉, 주황색 분포를 따른다고 가정하였을 때,
해당 데이터 셋들에 대한 likelihood를 수식적으로 위와 같이 표현할 수 있다.
따라서 만약 최적의 parameter theta'을 구하고자 한다면 위의 likelihood function P(x | theta)의 결과값이
가장 커지는 theta값으로 추정해주는 방법이 바로 이어서 설명할 MLE이다.
따라서 maximum likelihood estimation은 parameter를 추정해내는 방식중의 하나인데, likelihood function을
최대화 시킬 때의 파라미터값을 사용하는 방식이다.
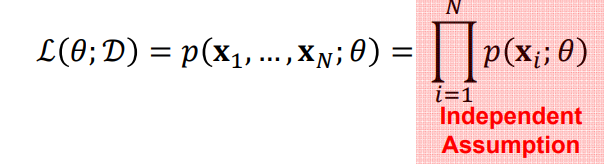
likelihood function L이고 구하고자하는 파라미터가 theta, D는 데이터의 분포를 의미.
N개의 independent and identical distributed instance를 가정하자.
수식적으로 편하게 만들어주기 위해서 자연로그를 위의 likelihood function에 취해준다.

그렇다면 likelihood function L(theta; D)를 최대화 시켜주는 theta값을 찾아줄 것인가? 미분을 사용하자.
likelihood function을 구하고자하는 파라미터 theta에 대하여 편미분을 실행해준다.

예시) N개의 가우시안 분포를 따르는 iid 데이터 샘플이 존재한다고 가정할 때, 평균값에 대한 최적의 추정값은 무엇인가? 또한 최적의 분산값은 무엇인가?

찾으려는 파라미터는 평균(mean)이다. 특정 mean을 갖을 때 모든 data sample들의 likelihood 기여도를 모두 곱해서
likelihood function을 구한다. 이 값에 자연 로그를 취해주고 mean에 대하여 편미분을 실행한 뒤, 그 값을
0이 되도록 설정해준다면 데이터들이 주어졌을 때, 최적의 평균값을 추정할 수 있다.
분산의 경우도 마찬가지로 likelihood function을 각 data sample들의 likelihood 기여도를 모두 곱해줘서 만들어준다.
그 뒤 분산에 대하여 편미분을 수행해줘서 최적의 분산값을 추정해준다.

MLE for Logistic Regression
Logistic Regression모델에서 구해줘야 하는 파라미터들은 계수 vector 베타이다.

(이전 노트(Lecture 5 (1) )에서 logistic regression이 Least Square Estimation을 사용하지 못하는 이유는 설명했다.)
그렇다면 이제 MLE를 사용하여, 즉 likelihood function을 최대화 시켜주는 베타 값들을 구하여 최적의 모델을 만들 것이다.
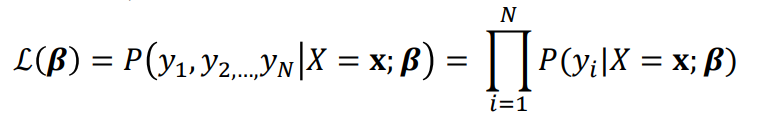
베타라는 파라미터의 likelihood function L(beta). 이는 input vector가 x가 들어왔을 때, 그리고 weight vector beta라는
식이 존재할 때, 특정 output들 y1, y2, ... yN들의 likelihood 기여도를 모두 곱한 값이다.
바이너리 outcome을 갖기 때문에, y = 1 이 나올 확률을 p라고 해준다면 y = 0이 나올 확률을 1-p가 나올 것이다.

따라서 likelihood function을 구해보면 다음과 같이 각 instance들의 likelihood 기여도의 총 곱셈으로 나타낼 수 있다.

pi는 i 번째 input을 넣었을 때 y = 1 일 나올 확률을 의미하며 수식적으로는 logistic regression식을 갖는다.

이때, likelihood function에 자연로그를 취해준다면 아래와 같이 최종적인 수식 전개가 가능하다.

likelihood function에 자연 로그를 취해준 수식을 cross entropy라고 부르며 logistic regression 모델에서의
objective function이 된다. 따라서 이 objective function을 최대화 시켜주는 weight vector 베타를 구해주는 것이
logistic regression 모델에서의 목표이다.

Objective function에 대한 최대값을 구할 것이기 때문에 Gradient Descent를 사용하여 square error의 최소값을 구하던
MSE과는 달리 gradient ascent를 사용한다.


하지만 굳이 Gradient Descent 방식이 있는데 ascent를 또 새로 만들어서 하기 귀찮으니까, 부호를 변화시켜줘서
ascent를 descent로 구현해준다.

Non - Linear Logistic Regression
Logistic Regression이 GLR의 일종이었기 때문에, non-linear한 basis들을 사용하여 non-linear하도록 만들어 줄 수 있다.
sigmoid 함수 안에 집어넣어주던 계수 베타와 인풋 벡터들의 선형 결합에서 인풋 벡터들을 그대로 넣어주는 것이 아닌,
basis function을 사용하여 Non - linear하게 만들어 주는 것이다.

예시) 2차원 feature vector를 polynomial order 2의 basis function을 이용하여 logistic regression을 적용한다.


즉, polynomial order 2의 basis 함수들을 사용하게 된다면, 원래는 2차원이던 feature vector가 5차원으로 변환된 것을
의미한다. 이렇게 고차원으로 변환된 경우에서 데이터들은 linear classifier처럼 작동할 수 있다.

위와 같이 2차원의 feature space에서는 boundary가 선형적이지 않은 타원형 커브인 것을 알 수 있다.
하지만 이를 다차원으로 변환시킨다면, 오른쪽 그림에서처럼 선형적인 hyperplane의 boundary를 갖는 것을 볼 수 있다.