Lecture 5 : Logistic Regression & Maximum Likelihood Estimation (1)
CONTENTS
- Logistic Regression
- Logistic Regression for Multiple Class problem
- Maximum Likelihood Estmation(MLE)
- Nonlinear Logistic Regressoin and Regularization
Logistic Regression
A machine learning model used for two-class pattern classification
본질적으로 2가지의 클래스를 분류하기위해서 사용되는 머신러닝 모델이며, 기본적으로 supervised Learning이다.
따라서 dataset이 주어질 때, input data X와 label Y가 주어지는데, label Y는 0 또는 1로 두가지만 존재한다.

어떠한 input X가 들어왔을 때, 어떠한 class Y일지를 판단하는 일종의 likelihood function를 input feature들의 linear
combination과 sigmoid 함수를 이용하여 표현해주는 것이 logistic regression이다.
아래의 값이 0.5보다 크면 output을 1로, 0.5보다 작으면 output을 0으로 추정해준다.
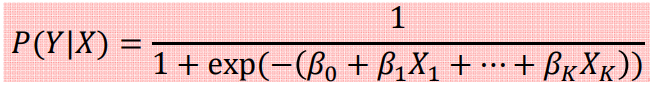
Assumptions in Logistic Regression
주어지는 training data는 {x(i), y(i) | i = 1, 2, ..., N}일 때
1. predicted output Y는 0 또는 1 만 존재하는 베르누이 분포를 따른다. 따라서 logitstic regression은
인풋을 받아서 0 또는 1이라는 두가지 경우의 output만 반환하기 때문에 classifier로 사용될 수 있다.

2. Instance들은 서로 independent하다.

3. Log odds(logit)은 predictor의 input으로 사용되는 변수들에 대하여 linear function이다.

따라서 logistic regression은 GLR의 일종이라고 할 수 있다.

최적의 모델을 구하기 위해서는 최적의 계수들 즉, 베타를 구해야한다. GLR에서 최적의 weight vector w를 구하던 것
처럼 Least Square Estimation을 사용하여 계수 벡터 베타를 구해보자.

이 알파는 아래와 같다.

하지만 이때, 자연로그 안 에 들어가는 posterior probability의 결과는 logistic regression에서는 항상 0 또는 1이 된다.
따라서 알파의 값은 양의 무한대가 되거나, 음의 무한대가 나올 수 밖에 없다.
즉, logistic regression과 같은 경우에는 LSE를 사용하여 최적의 계수 벡터를 구할 수 없다는 것을 확인할 수 있다.
Logistic Regression for Multi-class Classification
기본적으로 logistic regression은 two class classifier이기 때문에, 여러 클래스가 존재하는 경우에 logistic regression을
직접적으로 사용하지는 못한다. 따라서 새로운 approach를 사용하여 문제에 접근해야한다
1. One - vs - rest (one vs all) Approach

Trainin Stage에서는 c개의 클래스들에 대하여 각각의 train을 실시한다. 해당 Instance들이 class c에 속하는지 아닌지로
훈련을 진행한다.
Testing stage에서는 새로운 input x'을 C개의 classifier에 모두 넣어보고 가장 높은 확률(score)가 나온 class를 선택한다.

이러한 approach의 단점 : class가 많이 존재하는 경우에는 logistic regression 단계(즉, binary classification)에서
training data간에 dataset 수의 불균형이 발생하여 train model의 성능을 악화시킬 가능성이 있다.

2. One - vs - one

Training stage에서 C개의 class중 2개를 골라서 각각의 logistic regression을 진행한다,
Testing stage에서는 위에서 만든 모든 classifier에 새로운 input x'를 넣고 가장 많이 겹치는(most vote)를 선택한다.
이러한 approach의 단점 : vote가 동점이 나오는 경우에는 어떻게 최종 decision을 내려야할지 모른다. 또한 deccision
space가 충분히 넗아야한다